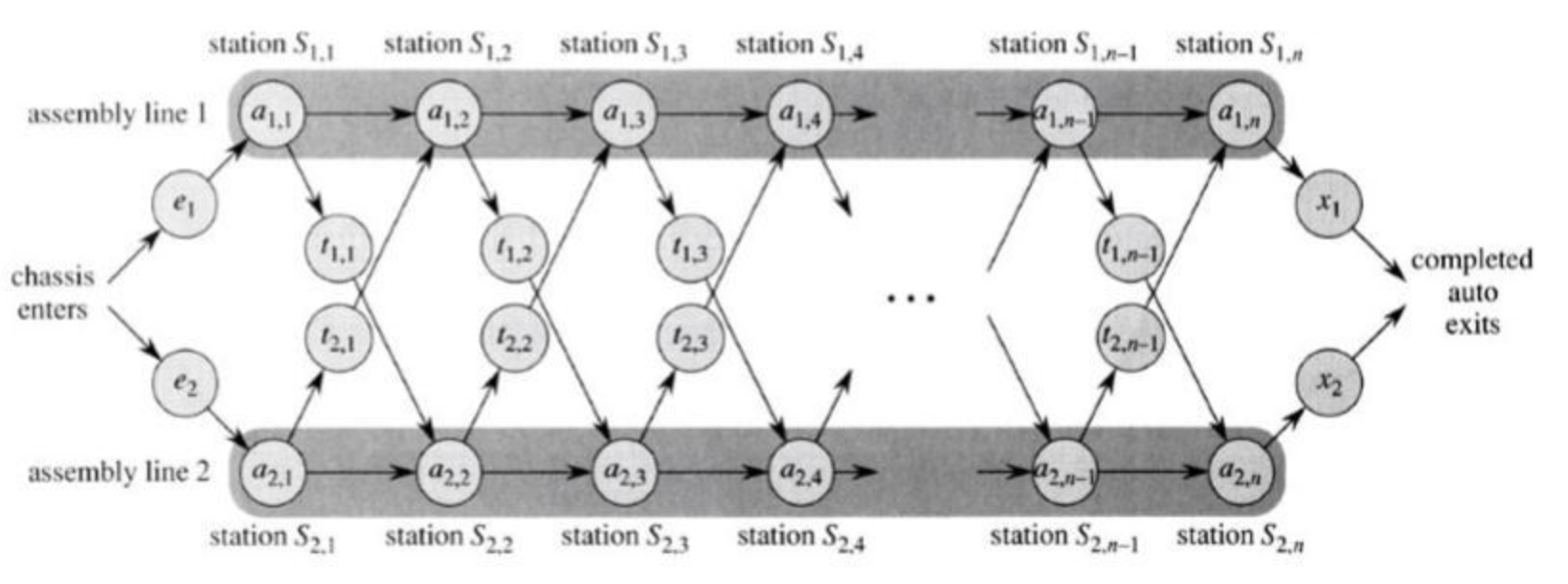
위의 라인은 S1, 아래 라인이 S2이다.
각 라인은 1부터 n까지의 공정이 있고, 이는 Si, j로 나타낸다. Si, j의 소요 시간은 각각 ai, j이다.
ei는 i번째 라인에 들어가는 데 소요되는 시간을 의미하고(ex. e1: line 1에 들어가는 데 소요되는 시간)
xi는 i번째 라인에서 작업을 다 마치고 나오는 데 소요되는 시간을 의미한다.
마지막으로 ti, j는, j번째 공정까지 마친 뒤 i번째 라인에서 다른 라인으로 교체하는 데 소요되는 시간이다.
f1[j]은, i번째 라인에서 진행하는 j 공정(Si, j)을 시작 지점으로 했을 때 가장 빠른 시간이다.
여기서 우리가 구해야 될 것은, f*, 즉 최종적으로 가장 빠른 시간을 저장하는 변수이다.
동적 계획법을 사용하여 접근하면 이 문제를 선형시간에 탐색할 수 있다.
# 필요한 것: a, t, e, x, n
# assembly line scheduling
n = int(input())
e1, e2, x1, x2 = 2, 4, 3, 2
f1, f2 = [0] * (n+1), [0] * (n+1)
a1 = list(map(int, input().split()))
a1.insert(0, 0)
a2 = list(map(int, input().split()))
a2.insert(0, 0)
t1 = list(map(int, input().split()))
t1.insert(0, 0)
t2 = list(map(int, input().split()))
t2.insert(0, 0)
f1[1] = e1 + a1[1]
f2[1] = e2 + a2[1]
fstar = 0
for i in range(2, n+1):
f1[i] = min(f1[i-1] + a1[i], f2[i-1] + t2[i-1] + a1[i])
f2[i] = min(f2[i-1] + a2[i], f1[i-1] + t1[i-1] + a2[i])
if f1[i] + x1 > f2[i] + x2:
fstar = f2[i] + x2
else:
fstar = f1[i] + x1
print(f1)
print(f2)
print(fstar)
공정이 1번부터 시작하기 때문에 편의상 각 리스트의 0번째 값을 0으로 주고 첫 번째 값부터 시작했다.
우선 각 라인의 첫 번째 공정을 수행하는 데 걸리는 시간을 부분해로 둔다. 첫 번째 공정에 소요되는 시간은
1) 라인 1의 경우: 1번째 라인에 들어가는 데 소요되는 시간 + S1,1의 소요 시간 = e1 + a1[1]
2) 라인 2의 경우: 2번째 라인에 들어가는 데 소요되는 시간 + S2,1의 소요 시간 = e2 + a2[1]
이다. 이를 부분해로 활용하고 2부터 n까지의 i에 대해서 각 라인에서의 소요 시간 f1[i], f2[i]는..
1) 라인 1의 경우:
라인 1의 이전 공정까지의 소요시간 + 라인 1의 i번째 공정의 소요 시간 = f1[i-1] + a1[i] 와
라인 2의 이전 공정까지의 소요시간 + 라인 2에서 i-1번째 공정까지 마친 뒤 i번째 라인에서 라인 1로 교체하는 데 소요되는 시간 + 라인 1의 i번째 공정의 소요 시간 = f2[i-1] + t2[i-1] + a1[i]
중에서 작은 값이고,
2) 라인 2의 경우:
라인 2의 이전 공정까지의 소요시간 + 라인 2의 i번째 공정의 소요 시간 = f2[i-1] + a2[i] 와
라인 1의 이전 공정까지의 소요시간 + 라인 1에서 i-1번째 공정까지 마친 뒤 i번째 라인에서 라인 2로 교체하는 데 소요되는 시간 + 라인 2의 i번째 공정의 소요 시간 = f1[i-1] + t1[i-1] + a2[i]
중에서 작은 값에 해당한다.
부분해를 구하고 재귀적으로 탐색하면 되는 것이다.
마지막으로, 이렇게 구해진 f1[i]의 값과 f2[i] 값에 대해서, f1[i] + 1번째 라인에서 작업을 마치고 나오는 시간 x1과 f2[i] + 2번째 라인에서 작업을 마치고 나오는 시간 x2 중 더 작은 값을 우리가 최종적으로 구하고자 하는 f* 값에 넣으면 된다.

각 값이 주어졌을 때 f1, f2와 fstar의 값을 구해보면..

잘 나온다. 각 공정이 1번째부터 시작하기 때문에 편의상 0번째 인덱스의 값을 0으로 넣었다.
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] m*n 격자 맨 아래 셀에에서 맨 위 셀로 이동하는 최단 경로 (0) | 2021.05.11 |
|---|---|
| [알고리즘] m*n 격자 (1, 1)에서 오른쪽, 위쪽으로만 이동하여 (m, n)로 가는 최단 경로 (0) | 2021.05.11 |
| [알고리즘] 입국심사에서 각 입국 심사자의 평균 대기 시간 구하기(심사대 k개, 최소힙 이용) (0) | 2021.05.01 |
| [알고리즘] 계단 오르기 3 (0) | 2021.05.01 |
| [알고리즘] 계단 오르기 2 (2) | 2021.04.30 |
