[Python] 이것이 취업을 위한 코딩 테스트다 with 파이썬 - 바닥 공사

1. 풀이

	n = int(input())
	# 2*1 = 1가지
	# 2*2 = 3가지 (각 1번씩)
	# 2*3 = 5가지 (2*2 3가지에 + 2 * 1 두번 더하기)
	# 2*4 = 11가지 (2*3 5가지에 2 * 2 두번 더하기)
	dp = [0] * 1001
	dp[1] = 1
	dp[2] = 3
	for i in range(3, n+1):
	dp[i] = (dp[i-1] + 2*dp[i-2]) % 796796
	print(dp[n])

view raw 바닥공사.py hosted with ❤ by GitHub

DP문제 중 계단 오르기와 더불어 기초에 해당하는 문제인데, 점화식을 찾지 못하면 좀 어려울 수도 있는 문제이다.

DP의 핵심은 우선 부분해를 구한 뒤 그것을 일반화하는 것이라고 생각한다. 그래서, 우선 쉽게 구할 수 있는 2*1과 2*2 각각을 구한 뒤에 3부터 일반화하여 구했다.

 

한번 생각해보자. 2 * 3의 바닥을 채우는 방법은 2 * 2의 바닥을 채우는 방법(2*1 2개, 1*2 2개, 2*2 1개 해서 총 3가지)에서 옆으로 1*2의 칸이 더 추가가 된 것이다. 이는 즉, (2 * 2의 바닥 채우기 + 1 * 2의 바닥 채우기) 순서와 (1 * 2의 바닥 채우기 + 2 * 2의 바닥 채우기) 순서를 합한 것이 총 2 * 3의 바닥을 채우는 방법이 되는 것이다.

 

이것을 일반화하면 i-2번째 줄 타일까지 다 채워져 있는 상황과 i-1번째 줄 타일까지 다 채워져 있는 상황을 생각하면 된다.

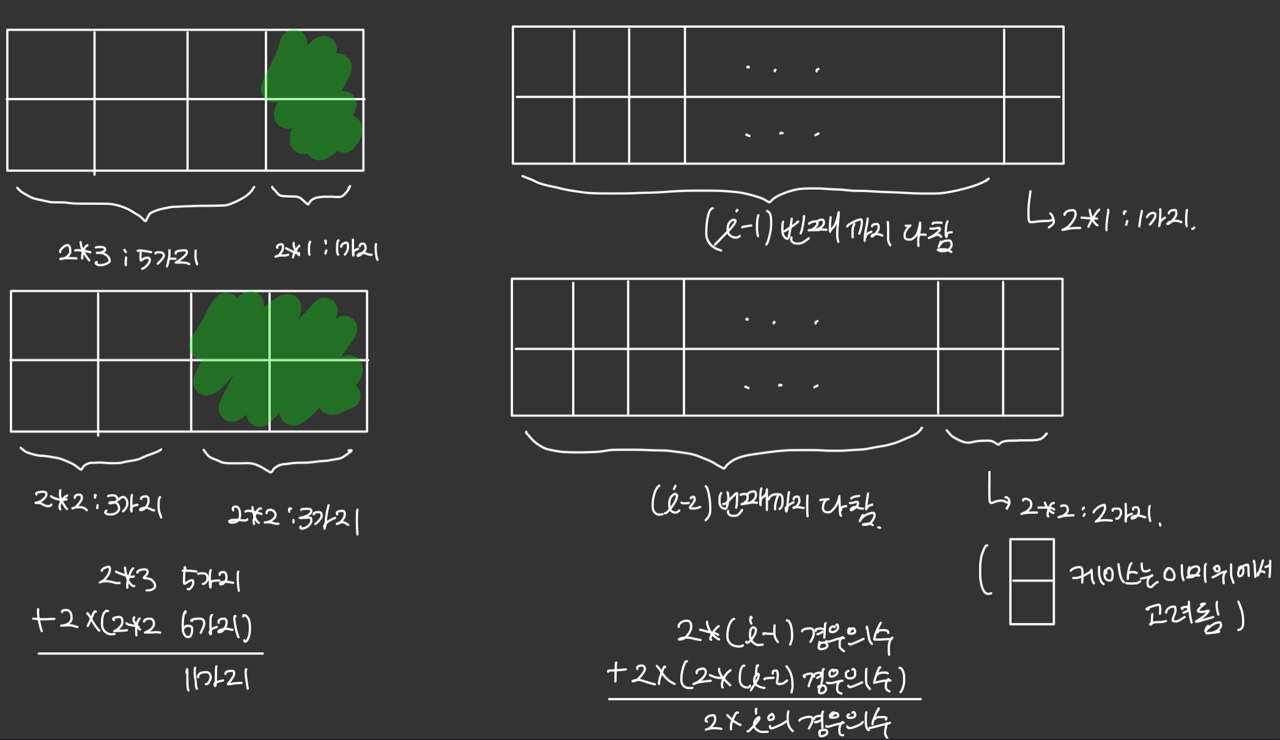
위 사진을 도식화하면..

      

      

      

    
    

      <python />
    
dp = [0] * 1001
dp[1] = 1
dp[2] = 3
for i in range(3, n+1):
	dp[i] = dp[i-1] + 2 * (dp[i-2])

이 된다.