링크 https://www.acmicpc.net/problem/2164 난이도(solved.ac 참고) 실버4 풀이 간단한 큐 문제이다. 문제에서 하라는 대로 q.pop() 해서 제일 위 값을 빼내고, 다시 한 번 제일 위의 값을 빼낸 다음 제일 아래로 넣는 과정만 반복한 다음 길이가 1이 되면 끝내고 그 수를 출력한다. 알고리즘을 한 달이 넘도록 풀지 않아서 다시 시작하려니 실력이 많이 죽었다. 다시 시작ㅜㅜ
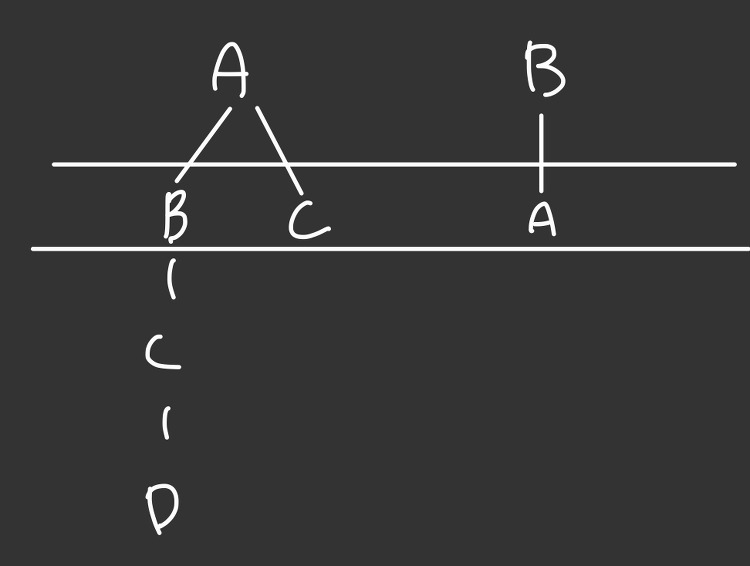
링크 https://www.acmicpc.net/problem/14725 난이도(solved.ac 참고) 골드2 풀이 딕셔너리 선언 후 값을 받아서 맨 앞의 숫자는 빼준 뒤에 차례차례 트리 형태처럼 계층을 가지게끔 add 함수를 재귀적으로 반복하면서 넣어준다. 3 2 B A 4 A B C D 2 A C 이 예시를 보게 되면 딕셔너리에 크게 B와 A가 들어가게 되고, A안에 다시 B, C, D 순으로 딕셔너리가 들어가며 다른 가지로 C가 들어가게 된다. 이 형태가 되는 것이다. 여기서 각각은 모두 딕셔너리이며 이렇게 add 함수를 통해 이러한 계층 구조를 완성시킨다. 왼쪽 가지를 보면 A의 value는 B와 C이고(모두 딕셔너리), B의 value는 C(딕셔너리), C의 value는 D(딕셔너리)이다. 마..
링크 https://www.acmicpc.net/problem/1516 난이도(solved.ac 참고) 골드3 풀이 이 문제는 위상정렬을 이용한 동적계획법 문제이다. 위상정렬의 알고리즘은 다른 곳에 이미 잘 나와있으므로 짧게 얘기하면 아래와 같은 방식이다. 1. 진입차수가 0인 노드를 큐에 넣는다. 2. 큐가 빌 때까지 다음의 과정을 반복한다. 1) 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다. 2) 새롭게 진입차수가 0이 된 노드를 큐에 넣는다. tower 배열의 마지막 값은 늘 -1이며 이것은 신경쓸 필요가 없으므로 그 이전 부분까지만 고려한다. tower의 첫번째 값은 해당 인덱스 번째 건물의 완성 시간을 나타내며 두번째 값부터 -1 전까지의 값의 개수만큼 진입차수를 갖고,..
링크 https://www.acmicpc.net/problem/6497 난이도(solved.ac 참고) 골드4 풀이 오랜만에 쓰는 알고리즘 포스팅이다. 이번에는 최소 스패닝 트리의 대표적인 예시인 크루스칼 알고리즘을 사용하여 문제를 풀었다. 크루스칼 알고리즘의 구현 과정은 아래와 같다. 1) 간선 데이터를 비용에 따라 오름차순으로 정렬 2) 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인 2-1) 사이클이 발생하지 않는 경우 최소 스패닝 트리에 포함 2-2) 사이클이 발생하는 경우 최소 스패닝 트리에 포함 X 3) 모든 간선에 대해 2)의 과정을 반복 find_parent 함수를 통해 매개변수 x의 루트 노드를 찾고, union_parent 함수를 통해 두 원소가 속한 집합을 합친다. p..
링크 https://www.acmicpc.net/problem/2960 난이도(solved.ac 참고) 실버4 풀이 쉬운 문젠데, 에라토스테네스의 체의 개념을 메모해두기 위해 포스팅한다. 에라토스테네스의 체는 N 아래의 소수를 빠르게 구하는 방법으로, 2부터 N까지의 인덱스가 True로 되어있는 배열들에 대해 i에 해당하는 값을 소수 배열에 넣은 뒤 그 i의 자연수 배수의 값들을 하나씩 False로 만들어주는 방식으로 소수를 구하는 방법이다. 예를 들어 2를 primes 배열에 넣는다면, 자연수 배수인 4, 6, 8, ... 의 값들을 모두 False 처리를 해주는 것이다. 이 문제는 K번째로 지워지는 수를 구해야 되었기 때문에 우선 result라는 배열에 지워질 값들을 전부 넣고 k-1번째 인덱스의 값..
링크 https://www.acmicpc.net/problem/20551 난이도(solved.ac 참고) 실버4 풀이 실버4라 만만하게 봤는데 생각보다 시행착오를 많이 겪었던 문제였다. 일단 이분 탐색을 사용해야 되는 문제였는데, 거기서도 lower_bound라는 개념을 익힐 수 있는 문제였다. lower_bound란 찾고자 하는 값이 가장 처음으로 나오는 위치를 찾는 함수다. 이분탐색에서 살짝만 바꿔주면 된다. 물론 당연히 이분탐색의 전제와 같이 sort가 되어있어야 한다. mid를 가운데 값으로 설정하고 target보다 작으면 mid+1로 왼쪽 범위 날리고, target보다 크면 right = mid - 1로 오른쪽 범위 날리고, 같을 경우가 문제다. [-1, 1, 3, 3, 3, 4, 5, 6, 6..
링크 https://www.acmicpc.net/problem/1149 1149번: RGB거리 첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 www.acmicpc.net 난이도(solved.ac 참고) 실버1 풀이 다이나믹 프로그래밍 문제다. DP 배열을 선언하고 첫 값은 input값으로 받은 street의 첫 열을 그대로 갖다 붙인다. 다음 열로 넘어갈 때 각 dp의 값은, 이전 열의 같은 행 값이 아닌 다른 행의 값들에 + 현재 위치한 인덱스의 street값을 더해준 것 중 더 작은 것을 넣어준다. 이 과정을 반복하고 가장 마지막 열..
링크 https://www.acmicpc.net/problem/2166 난이도(solved.ac 참고) 골드5 풀이 다각형의 넓이를 구하기 위해서 우리가 고등학교 시절에 수학시간에 배웠던 신발끈 공식을 사용해야 한다. 신발끈 공식이란 n각형이 있을 때에 (x1, y1), (x2, y2), .., (xn, yn)이 있다고 할 때 이 넓이는 1/2 * | (x1*y2 + x2*y3 + .. + xn-1*yn + xn*y1) - (y1*x2 + y2*x3 + .. + yn-1*xn + yn*x1) | 와 같다는 공식이다. 자세한 건 나무위키를 참조하기 바란다. 이 문제는 이 신발끈 공식을 구현하면 되는 문제였다. 전부다 구하고 마지막에 2로 나눠준 뒤 절댓값을 씌워주면 해결할 수 있는 어렵지 않은 문제였다.
링크 https://www.acmicpc.net/problem/1092 난이도(solved.ac 참고) 골드5 풀이 가장 높은 중량을 들 수 있는 크레인에 가장 무거운 박스를 배치하면 된다. 크레인에 대한 반복문이 끝나면 1회 순회한 것이므로 while문 직후에 time이라는, 우리가 답으로 출력할 변수의 값을 1씩 증가해준다. 그리고 크레인의 값이 더 클 경우에 break을 함으로써 weight에 대해 불필요하게 남은 box에 대한 반복문을 돌 필요가 없게끔 하였다(break없이 돌면 안돼서 넣은 것이기도 함).
링크 https://www.acmicpc.net/problem/2170 난이도(solved.ac 참고) 골드5 풀이 문제를 보자마자 생각했던 것은 1) 처음 input으로 받은 y - x의 값을 길이를 나타내는 변수인 leng에 초기값으로 두고, 이 y값을 target으로 설정한 다음 2) 정렬이 되어있다는 전제 하에, 이 첫번째 y와 같은 x가 나올 때까지 leng의 값에 (y의 값들 - target)을 더해주고 target을 각 y로 바꿔주는 방식으로 업데이트하자 3) 계속 target값을 업데이트하던 와중에 새로운 x값이 target보다 클 경우 선이 끊어져 있다는 뜻이므로 여기서는 leng에 (새로운 y값 - 새로운 x값)을 더해준 다음 target은 똑같이 새로운 y값으로 바꿔주자 라는 것이었다..