알고리즘 및 운영체제 정규학기 수업 대비 자료구조 공부를 하고 있다.
자료구조
트리(Tree)
데이터의 상-하 관계(계층적 관계)를 저장하는 자료 구조이다.
컴퓨터 폴더 구조 및 클래스 상속 관계 등을 예로 들 수 있다.

배열 및 링크드 리스트: 선형적 자료 구조 (앞과 뒤 라는 순서를 저장할 수 있음)
해시 테이블: 데이터 관계를 저장하지 않음
-> 계층적 데이터 관계를 저장하기에 적합하지 않다. 트리를 통해 저장할 수 있다.
트리 노드는 하위 관계가 있는 노드를 가리키는 레퍼런스를 갖는다.

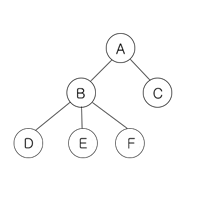
B와 C를 A의 자식 노드로 만들고 싶다고 해보자. 그럴 경우 A에 B와 C를 가리키는 레퍼런스를 저장하면 된다. 트리에서는 보통 이 레퍼런스를 화살표로 나타낸다.

더 많은 노드를 만들고, 이 노드들 사이에 부모-자식 관계를 만들어주면 훨씬 복잡한 데이터를 저장할 수 있다.
한편 이 노드들 중에, 가장 위에 있는 노드 A를 루트 노드(root node)라고 부른다. 이 노드에서부터 찾아가면 모든 노드들을 찾아갈 수 있다.
트리 용어

-
root 노드(뿌리 노드): 트리의 시작 노드, 뿌리가 되는 노드이다. 보통 트리를 표현할 때 위 그림처럼 가장 위에 root 노드를 놓는 방식으로 나타낸다.
-
부모 노드: 특정 노드의 직속 상위 노드이다. 노드
G, J, K가 있는 노란색 박스를 살펴보면G가J와K의 부모 노드이다. -
자식 노드: 특정 노드의 직속 하위 노드이다. 부모 노드와 반대되는 개념이다. 노드
G, J, K가 있는 노란색 박스를 살펴보면J와K가G의 자식 노드이다. -
형제 노드: 같은 부모를 갖는 노드이다.
D와E는 둘다 그 부모가B인데, 이럴 때D와E는 서로 형제 노드이다. -
leaf 노드(잎/말단 노드): 자식 노드를 갖고 있지 않은, 가장 말단에 있는 노드이다. 트리의 끝에 있다고 해서 root(뿌리) 노드와 반대되는 표현으로 leaf(잎) 노드라고 부른다. 위 그림에서 노란색 박스로 둘러싼
F가 leaf 노드이다.F뿐만 아니라D, H, I, J, K모두 leaf 노드이다. -
깊이: 특정 노드가 root 노드에서 떨어져 있는 거리이다. 깊이는 해당 노드로 가기 위해서 root 노드에서 몇 번 아래로 내려와야 하는지를 나타낸다.
-
레벨: 깊이 + 1. 깊이와 거의 똑같은 개념이다. 그냥 깊이에 1을 더한 값이다. 레벨 1에 있는 노드들, 레벨 2에 있는 노드들, ... 이런 식으로 특정 깊이인 노드들을 묶어서 표현할 때 사용하는 용어이다.
-
높이: 트리에서 가장 깊이 있는 노드의 깊이이다. 위 그림의 트리에서는
H, I, J, K가 가장 깊이 있는 노드들이고 그 깊이는 모두 3이다. 그래서 트리의 높이는 3이다.

- 부분 트리(sub-tree): 현재 트리의 일부분을 이루고 있는 더 작은 트리를 말한다.위 그림의 트리는
root노드가A인 트리이다. 이 트리를 좀 더 작은 단위로 쪼개보면 더 작은 부분 트리들을 발견할 수 있다. 예를 들어 위 그림의 노란 색 큰 박스 안을 보자. 노란색 큰 박스 안에는C가 root 노드인 트리가 있는데, 이런 것을 바로 부분 트리라고 한다.C는A의 오른쪽 자식이다. 그래서 노란색 큰 박스 안에 있는 부분 트리를A의오른쪽 부분 트리라고 한다. 특정 노드를root노드라고 생각하고 바라본다면 여러 가지 부분 트리들을 발견할 수 있다. 하나의 전체 트리에 여러 부분 트리들이 존재하는 것이다.
트리의 활용
-
컴퓨터 과학의 다양한 문제들을 기발하게 해결할 수 있다.
ex) 주어진 데이터를 순서대로 재정렬시키는 문제, 용량이 큰 파일을 더 작은 파일로 압축시키는 압축 문제 등 -
흔히 사용하는 다양한 추상 자료형을 구현하는 데 쓸 수 있다.
- 계층적 데이터 뿐만 아니라 다양한 데이터를 저장하는 데 쓰는 추상 자료형을 구현할 수 있다.
- 계층적 관계가 있는 데이터를 컴퓨터에서 사용할 수 있다.
이진 트리
각 노드가 최대 2개의 자식만을 가질 수 있는 트리

이진 트리 구현
트리의 기본 데이터 단위인 노드(Node)를 만들어줘야 한다.

해당 형태를 가진 트리를 만들어 볼 것이다.
class Node:
"""이진 트리 노드 클래스"""
def __init__(self, data):
"""데이터와 두 자식 노드에 대한 레퍼런스를 갖는다."""
self.data = data
self.left_child = None
self.right_child = None
# 노드 인스턴스 생성
root_node = Node(2)
node_B = Node(3)
node_C = Node(5)
node_D = Node(7)
node_E = Node(11)
# B와 C를 root 노드의 자식으로 지정
root_node.left_child = node_B
root_node.right_child = node_C
# D와 E를 B의 자식으로 지정
node_B.left_child = node_D
node_B.right_child = node_E
# root 노드에서 왼쪽 자식 노드 받아오기
test_node_1 = root_node.left_child
print(test_node_1.data)
# 노드 B의 오른쪽 자식 노드 받아오기
test_node_2 = node_B.right_child
print(test_node_2.data)이진 트리의 종류
정 이진 트리 (Full Binary Tree)
- 모든 노드가 2개 또는 0개의 자식을 갖는 이진 트리

왼쪽 이진 트리에서 12의 자식은 10밖에 없고, 10은 자식이 2밖에 없다. 그러므로 왼쪽은 정 이진 트리가 아니다.
반면에 오른쪽은 아예 없거나 쌍으로 2개의 자식들을 갖고 있으므로 정 이진 트리이다.
완전 이진 트리(Complete Binary Tree)

이진 트리에서 노드의 깊이를 레벨이라고 해보자. 이진 트리 중에서도 마지막 레벨 직전의 레벨까지는 모든 노드들이 다 채워진 트리를 완전 이진 트리라고 한다. 한 가지 조건이 더 있는데, 마지막 레벨에서는 노드들이 다 채워질 필요는 없더라도, 왼쪽부터 오른쪽 방향으로는 노드들이 다 채워져야 한다. 정리하자면,
- 마지막 레벨을 제외한 모든 레벨이 다 차 있다.
- 마지막 레벨은 왼쪽에서 순서대로 차 있다.

왼쪽의 이진 트리는 1번 조건을 만족하지 못했고, 오른쪽의 이진 트리는 2번 조건을 만족하지 못했으므로 둘 다 완전 이진 트리가 아니다.
완전 이진 트리의 높이

완전 이진 트리에 저장된 노드가 n개라고 할 때, 높이는 항상 log(n)에 비례한다.
완전 이진 트리의 각 레벨에는 노드가 몇 개씩 있을까?
- 레벨 1에 1개
- 레벨 2에 2개
- 레벨 3에 4개
... - 레벨 n에 2^{n-1}개
이런 식으로 노드 개수가 늘어난다. 레벨이 하나씩 증가할 때마다 이전 레벨에 있는 노드 개수의 2배를 더 담을 수 있다.
이를 표로 정리하면,
| 레벨 | 총 노드수 최솟값 | 총 노드수 최댓값 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1+1 | 1+2 |
| 3 | 1+2+1 | 1+2+4 |
| 4 | 1+2+4+1 | 1+2+4+8 |
| 5 | 1+2+4+8+1 | 1+2+4+8+16 |
| ... | ... | ... |
| n | 1+2+4+...+2^{h-1}+1 |
1+2+4+...+2^{h} |
이 표를 통해, 완전 이진 트리의 높이를 h, 그 노드 수를 n이라고 할 때
2^{h} <= n <= 2^{h+1}-1
2^{h} <= n < 2^{h+1}
이고, 각 항에 log를 씌우면
h <= log(n) < h+1이 된다.
이걸 보면, 완전 이진 트리의 높이는 노드 수에 log를 취한 값보다 작은 정수 중에서 최대의 정수임을 알 수 있다.
포화 이진 트리 (Perfect Binary Tree)

포화 이진 트리는 위 트리처럼 모든 레벨이 빠짐없이 다 노드로 채워져 있는 이진 트리이다. 모든 레벨이 완벽하게 다 채워져 있기 때문에 영어로는 perfect binary tree라고 부른다. 포화 이진 트리는 기본적으로 정 이진 트리와 완전 이진 트리의 특성을 모두 갖는다.
포화 이진 트리는
- 높이가 0이면 노드 수가 1개
- 높이가 1이면 노드 수가
(1+2)개 - 높이가 2이면 노드 수가
(1+2+4)개 - 높이가 h이면 노드 수가
(1+2+4+...+2^{n})개
등비수열의 합을 계산하면,
n = 2^{h+1} - 1이 되고, 각 변에 1을 더해주면,
n + 1 = 2^{h+1}을 만족하게 된다.
위 그림의 포화 이진 트리에서 노드의 수는 총 7인데, 이를 n+1 = 2^{h+1}에 대입해보면, 8 = 2^{h+1} => h = 2 라는 결과가 나온다. 이렇게 포화 이진 트리는 그 높이나 노드의 수, 둘 중에서 하나만 알아도 나머지 하나의 값을 바로 구할 수 있다.
완전 이진 트리 배열(파이썬 리스트)에 저장하기

이러한 완전 이진 트리가 있다고 하자. 이 완전 이진 트리는 아래처럼 리스트에 저장할 수 있다.
complete_binary_tree = [None, 1, 5, 12, 11, 9, 10, 14, 2, 10][0]을 None으로 두고 1번째 인덱스부터 root 노드를 시작으로, 그 다음에 깊이가 1인 노드들을 왼쪽에서 오른쪽 방향 순으로, 그 다음에 깊이가 2인 노드들을 왼쪽에서 오른쪽 방향 순으로 차례대로 리스트에 저장하면 된다. 이에 따라 [1] = 1, [2] = 5, ... 이 된다.
자식 노드 찾기
위의 그림에서, [2](노드 5)의 왼쪽 자식 노드를 찾고 싶다고 해 보자. 먼저 [2]에 2를 곱하면 [4]가 된다. 그 다음 리스트의 [4]에 있는 노드를 찾으면 된다. 노드 11인데, 이는 정확히 노드 5의 왼쪽 자식 노드이다.
이번에는 3(노드 12)의 오른쪽 자식 노드를 찾고 싶다고 해 보자. 먼저 [3]에 2를 곱하면 [6]이 된다. 그 다음 오른쪽이므로 +1을 해주면 [7]인데, 여기서 [7]은 노드 14이다.
부모 노드 찾기

여기서 [6](노드 10)의 부모를 찾으려면 6을 2로 나누면 된다. [3]에 있는 노드 12이다.
자식 노드의 인덱스가 홀수라면? [7](노드 14)의 부모 노드를 찾으려면, 우선 7을 2로 나눠준 후 나머지를 버리면 된다. 그럴 경우 몫인 [3]에 있는 노드 12가 된다.
완전 이진 트리는 그것이 가지는 특수한 2가지 성질:
- 마지막 레벨 직전 레벨까지는 노드들로 가득 차 있음
- 마지막 레벨은 왼쪽에서 오른쪽 방향으로 노드들로 가득 차 있어야 함(오른쪽은 비어있어도 되지만 왼쪽은 비어있으면 안됨)
때문에 이렇게 각 노드를 리스트에 저장한 후에도 부모 노드와 자식 노드를 손쉽게 찾을 수 있다.
트리 순회
- 자료 구조에 저장된 모든 데이터를 도는 것
def traverse(node):
"""트리를 순회하면서 출력하는 함수"""
...
traverse(root_node) # 이러한 코드를 통해 호출한다.- 재귀적으로 왼쪽 부분 트리 순회

traverse(root_node.left_child)의 형태로 순회한다.
왼쪽 부분 트리를 순회하는 경우 그림의 박스 내부를 순회하는데, 여기서는 traverse(node) 내에 다시 한 번 node.left_child를 파라미터로 받아 traverse(node.left_child) 의 순회 과정을 거치게 된다.
- 재귀적으로 오른쪽 부분 트리 순회

traverse(root_node.right_child)의 형태로 순회한다.
오른쪽 부분 트리를 순회하는 경s우 그림의 박스 내부를 순회하는데, 여기서는 traverse(node) 내에 다시 한 번 node.right_child를 파라미터로 받아 traverse(node.right_child) 의 순회 과정을 거치게 된다.
- 현재 노드 데이터를 출력

print(node.data)만 해주면 된다.
트리 순회: pre-order
아래의 순서대로 호출하는 순회 방법
- 현재 노드 데이터를 출력한다.
- 재귀적으로 왼쪽 부분 트리를 순회한다.
- 재귀적으로 오른쪽 부분 트리를 순회한다.
pre(~전에)-order, 즉 부분 트리 순회 전에 현재 노드를 출력하는 순회를 말한다.

루트 노드 출력 -> 왼쪽 부분 트리 노드 출력 -> 오른쪽 부분 트리 노드 출력 의 순서임
traverse(root_node)를 써서 위의 과정을 진행한다고 해 보자.
traverse(root_node)
현재 노드 출력으로 인해 F가 출력됨
traverse(node_b)
현재 노드 출력으로 인해 B가 출력됨
traverse(node_a)
현재 노드 출력으로 인해 A가 출력됨. 왼쪽과 오른쪽 부분 트리가 없으므로 아무것도 하지 않아도 됨. B의 왼쪽 트리 모두를 순회했으므로 이제 오른쪽 부분 트리를 순회한다.
traverse(node_d)
현재 노드 출력으로 인해 D가 출력됨
traverse(node_c)
현재 노드 출력으로 인해 C가 출력됨. 왼쪽과 오른쪽 부분 트리가 없으므로 아무것도 하지 않아도 됨. D의 왼쪽 트리 모두를 순회했으므로 이제 오른쪽 부분 트리를 순회한다.
traverse(node_e)
현재 노드 출력으로 인해 E가 출력됨. 마찬가지로 부분 트리가 더이상 없으므로 D의 오른쪽 부분 트리를 모두 순회했음. B도 마찬가지. 즉 F의 왼쪽 부분 트리를 전부 순회한 것이다.
traverse(node_g)
현재 노드 출력으로 인해 G가 출력됨. 왼쪽 부분 트리가 없으므로 오른쪽 부분 트리를 순회한다.
traverse(node_i)
현재 노드 출력으로 인해 I가 출력됨
traverse(node_h)
현재 노드 출력으로 인해 H가 출력됨. 더이상 부분 트리가 없고 I의 오른쪽 부분 트리 또한 없으므로 ,결과적으로 F의 오른쪽 부분 트리르 전부 순회하게 되었다.
최종 출력: F, B, A, D, C, E, G, I, H
트리 순회: post-order
아래의 순서대로 호출하는 순회 방법
- 재귀적으로 왼쪽 부분 트리를 순회한다.
- 재귀적으로 오른쪽 부분 트리를 순회한다.
- 현재 노드 데이터를 출력한다.
pre(~후에)-order, 즉 부분 트리 순회 후에 현재 노드를 출력하는 순회를 말한다.

최종 출력: A, C, E, D, B, H, I, G, F
트리 순회: in-order
아래의 순서대로 호출하는 순회 방법
- 재귀적으로 왼쪽 부분 트리를 순회한다.
- 현재 노드 데이터를 출력한다.
- 재귀적으로 오른쪽 부분 트리를 순회한다.
in(~안(사이)에), 즉 부분 트리 순회 사이에 현재 노드를 출력하는 순회를 말한다.

최종 출력:A, C, E, D, B, F, G, I, H (X)A, B, C, D, E, F, G, H, I (O)
데이터간 계층적 관계를 저장하는 트리도 순회를 하면 노드들 사이에 선형적 순서를 만들 수 있다.
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] BFS 알고리즘 (0) | 2021.03.09 |
|---|---|
| [자료구조] 그래프 (기본 그래프, 인접 행렬, 인접 리스트) (0) | 2021.03.08 |
| [자료구조] 이진 탐색 트리(2) (삭제, 시간 복잡도) (0) | 2021.03.04 |
| [자료구조] 이진 탐색 트리(1) (탐색, 삽입, 삭제) (0) | 2021.03.02 |
| [자료구조] 힙, 우선 순위 큐 (0) | 2021.03.02 |