문제 기술
2) 다음과 같은 형태의 일방통행 도로망에서 호텔에서 공항까지 가는 버스를 운행하고 있다. 호텔에서 공항까지 가는 도로망의 구조는 다음과 같다.
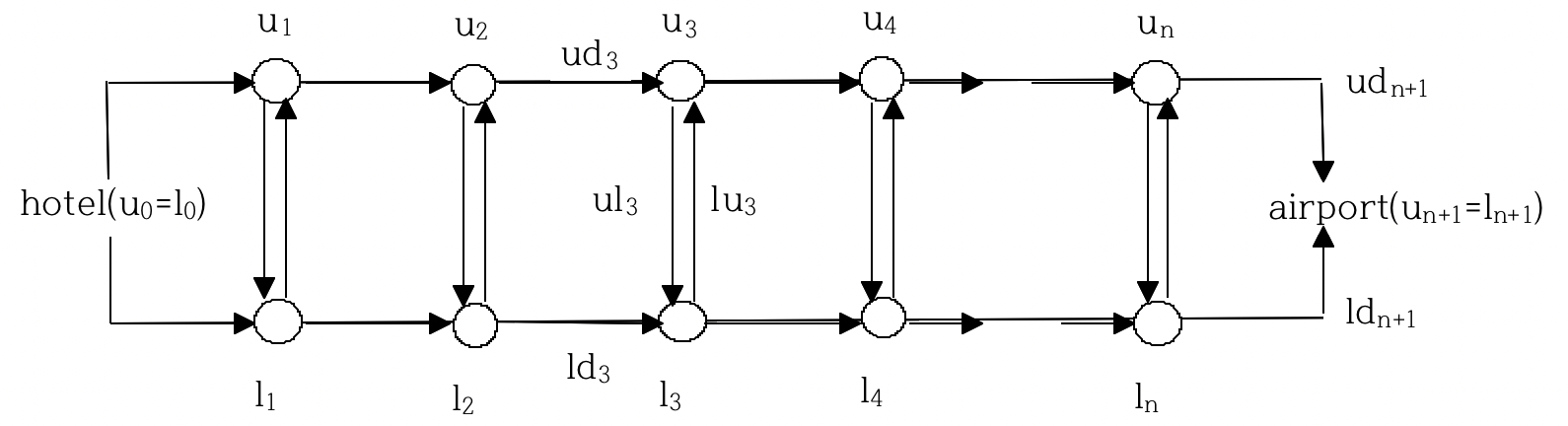
위쪽 도로에 n개 교차로 u1, u2, …, un이 있고, 아래쪽 도로에 n개 교차로 l1, l2, …, ln이 있다. u0(=l0)는 호텔을 나타내고, un+1(=ln+1)은 공항을 나타낸다. 그리고 i <= i <= n+1에 대해 위쪽 교차로 ui-1에서 ui까지 도로를 지나는데 걸리는 시간 udi과, 아래쪽 교차로 li-1에서 li까지 도로를 지나는데 걸리는 시간 ldi과, 그리고 교차로 ui에서 li까지 도로를 지나는데 걸리는 시간 ul와, 교차로 li에서 ui까지 도로를 지나는데 걸리는 시간 lui가 주어진다.
동적계획법을 이용하여 호텔에서 공항까지 가는데 걸리는 최소시간을 구하는 프로그램을 작성하시오.
(제약조건: 부분문제 해의 값을 저장하기 위한 메모리 공간을 O(1) 크기만큼 사용해야 함)
입력
첫 번째 줄에 위쪽 교차로 개수 n이 주어진다. 두 번째 줄에 1 <= i <= n+1에 대해 ui-1에서 교차로 ui까지 도로를 지나는데 걸리는 시간 uid들이 차례로 주어진다. 세 번째 줄에 1 <= i <= n+1에 대하여 li-1에서 교차로 li까지 도로를 지나는데 걸리는 시간 ldi들이 차례로 주어진다. 네 번째 줄에 1 <= i <= n에 대하여 ui에서 li까지 도로를 지나는데 걸리는 시간 uli들이 차례로 주어지고, 다섯 번째 줄에 1 <= i <= n에 대하여 li에서 ui까지 도로를 지나는데 걸리는 시간 lui들이 차레로 주어진다.
출력
호텔에서 공항까지 가는데 걸리는 최소시간을 출력한다.
입력 예
n = 3

3
4 5 2 7
1 4 7 5
1 2 1
2 1 1
출력 예
14
나의 코드
n = int(input())
u, l, star = [0] * n, [0] * n, [0] * n
ud = list(map(int, input().split())) # ud, ld, ul, lu 전부 input값을 리스트로 받아옴
ld = list(map(int, input().split()))
ul = list(map(int, input().split()))
lu = list(map(int, input().split()))
u[0] = min(ud[0], ld[0] + lu[0]) # 위에서 오는 경우와 아래에서 오는 경우 중 작은 값을 u, l의 base case로 지정함
l[0] = min(ld[0], ud[0] + ul[0])
star = min(u[0] + ud[1], l[0] + ld[1]) # 위에서 정한 u, l의 base case에 그 다음 인덱스의 값을 더한 값을 star로(O(1)) 지정함 (base case)
ud_last = ud[-1]
ld_last = ld[-1]
for i in range(1, n):
u[i] = min(u[i-1] + ud[i], l[i-1] + ld[i] + lu[i]) # 마찬가지로 위에서 오는 경우와 아래에서 오는 경우 중 작은 값을 u[i]와 l[i]로 지정. 이 때에 base case와의 차이점이라면 재귀 형태를 갖기 때문에 아래에서 위로 / 위에서 아래로 가는 경우 i-1번째의 u, l 값에 기반한다는 점이다.
l[i] = min(l[i-1] + ld[i], u[i-1] + ud[i] + ul[i])
if u[i] + ud[i+1] > l[i] + ld[i+1]: # u[i], l[i] 각각에 다음 ud, ld의 인덱스를 더한 값 중 더 작은 값을 star[i]로 지정한다. 결과적으로 for문이 다 끝나면 마지막 ud, ld를 더해준 값 중 더 작은 값이 최소 시간이 된다.
star = l[i] + ld[i+1]
else:
star = u[i] + ud[i+1]
print(star) # for문이 다 끝났을 때 구해진 star를 그대로 출력부분해가 저장되는 변수 star가 O(1)이어야 하므로, 배열이 아닌 한 가지의 값 형태로 저장한다.
앞서 올렸던 Assembly Line Scheduling 문제와 흡사하지만, 최종 목적지가 ui+1, li+1의 형태로 되어있다는 점에서 살짝 차이점이 존재한다.
ul의 경우 (위에서 오는 비용)와 (li까지의 비용 + 위로 오라오는 비용) 중 작은 값을 지정했고, 매 for문이 끝날 때마다 (u[i] + 다음 경로로 이동하는 비용 ud[i+1]) 과 (l[i] + 다음 경로로 이동하는 비용 ld[i+1]) 중 작은 값을 star라는 변수에 넣어줬고, 이렇게 하면 마지막 for문이 끝났을 때 최종 목적지까지 가는 최단 비용이 출력된다.
'CS > 알고리즘' 카테고리의 다른 글
| [Python] 미로 찾기(BFS) (0) | 2021.06.01 |
|---|---|
| [Python] BOJ 1439번 - 뒤집기 (0) | 2021.05.19 |
| [알고리즘] m*n 격자 맨 아래 셀에에서 맨 위 셀로 이동하는 최단 경로 (0) | 2021.05.11 |
| [알고리즘] m*n 격자 (1, 1)에서 오른쪽, 위쪽으로만 이동하여 (m, n)로 가는 최단 경로 (0) | 2021.05.11 |
| [알고리즘] 동적 계획법 - Assembly Line Scheduling using Python (0) | 2021.05.07 |
